داليتي سكول -

Daliaty School

صفحة البيت  |

بايثون – פיתון – python

مساحة الدائرة ومحيط الدائرة. 

(שטח עיגול והיקף של מעגל)

· نرمز إلى نصف قطر الدائرة بالحرف r  (Radius) · نرمز إلى قطر الدائرة بالحرف d  (diameter) · القطر يساوي مرتين نصف القطر ، d=2·r · النسبة بين محيط الدائرة L وقطر الدائرة d هي نسبة ثابتة    ،        ،   (π=3.14)

محيط الدائرة:
مساحة الدائرة:

تماريــــــــــن

سؤال:

إحسب المحيط والمساحة لدائرة نصف قطرها 8 أمتار.

المحيط: L=2πr L=2·8·π L50.3 m

المساحة: S=πr^2 S=π·8^2 S64π (m^2)

سؤال:

إحسب المحيط والمساحة للدوائر المعطاة.

= π · (9·2) = 56.5cm

= π · 9^2 = 254.34 cm^2

سؤال:

إحسب المحيط والمساحة للدوائر المعطاة.

= π · (3·2) = 18.8m

= π · 3^2 = 28.3 cm^2

سؤال:  (مساحة ومحيط دائرة) 

استعمل  = 4.14π  لإجاد مساحة الدوائر التالية:

سؤال:  (مساحة دائرة)

تذكر: لكل دائرة، القطر هو مرتين نصف القطر، القطرd = 2 · r القطر d = 2 · 3 = 6 cm المحيط: L = π · d   = π · 8   = 25.13 CM المساحة: A = π·4^2= π·16 = 16 π    = 16 · 3.14 = 28.27 cm^2
القطر d،  d = 2r القطر d = 2·r القطر d = 2 · 3 = 6 cm L = π·d L = π·6 = 6 π L = 6·3.14 = 18.85cm

سؤال:

جد المساحة والمحيط للدائرة المعطاة (أكمل الناقص)

S = π · 8  cm²

L = 8 ·π cm

سؤال:

جد مساحة الدائرة المعطاة:

(a)  120 (b) 113 (c) 37.68 (d)   36 الحل: ( b )

S =  cm^2

احسب محيط دائرة طول قطرها 50 سم.

الحل:

C = r × 3.14

C = 50 × 3.14

C = سم 157

طول محيط الدائرة هو 157 سم

طاولة مستديرة طول نصف قطرها 5م. ارادت أم شراء شرشف لتغطيتها.

جد مقدار مساحة القماش؟؟

الحل:

المطلوب: إيجاد مساحة الشرشف (الدائرة).

مساحة القماش اللازمة هي 78.5 سم مربع لتغطية الطاولة

S = r × r × 3.14 S = 5 × 5 × 3.14 S = سم مربع 78.5

ذ

سؤال:

أمامكم 5 أشكال. رتبوهم حسب كبر المساحات وحسب كبر المحيطات.

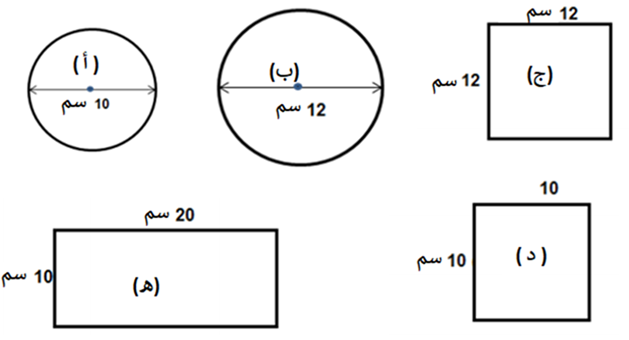
الحل:

(أ) S=π·5·5 = 25π = 25·3.14 = 78.5 cm²

(ب) S=π·6·6 = 36π = 36·3.14 = 113.04 cm²

(ج) S=12² = 12·12 = 144 cm²

(د) S=10² = 10·10 = 100 cm²

(ه) S=10·20 = 200 cm²

(أ) L=2·π·5 = 10 · π = 10·3.14 = 31.4 cm²

(ب) L=2·π·6 = 12·π = 12·3.14 = 37.68 cm²

(ج) L=4·12 = 48 cm

(د) L=4·10 = 40 cm

(ه) L=2·(20+10) = 60 cm

سؤال:

ما هو نصف قطر الدائرة التي محيطها 16π؟  

أ.  32 سم. ب. 16 سم.  ج. 8 سم.  د. 2 سم.

الحل:  (ج) 8 سم

L = 2·π·r 

--------------------

2·π·r = 16π    / : π

2·r = 16           / : 2

r = 8 cm²

سؤال:

معطى نصف دائرة طول نصف قطرها 4 وحدات.

أ. جدوا مساحة الدائرة. ب. جدوا مساحة نصف الدائرة. ج. جدوا محيط الدائرة. د. جدوا محيط نصف الدائرة.

الحل:

S_دائرة = π·r² =  π·r·r

S_دائرة =π·4·4 = 16π

S_{نصف دائرة} = 16π : 2 = 8π cm²

Lدائرة =2·π·r ==>  2·π·4 = 8π cm Lنصف دائرة = 8π : 2 + 8 =  4π + 8

محيط ومساحة نصف دائرة:

سؤال:

جد محيط الشكل التالي (طول الخط الخارجي): محيط الشكل مكون من: نصف محيط الدائرة + القطر.

الحل:

محيط الدائرة:

L = πd = π · 8 = 3.14 · 8 = 25.12 cm

نصف محيط الدائرة: 25.12 : 2 = 12.56cm

محيط الشكل المطلوب:

p =  12.56   +    8    = 20.56 cm

سؤال:

جد مساحة الشكل التالي: مساحة الشكل هو نصف مساحة الدئرة. A = πr^2   = ·(π · 4 · 4)   = 25.13cm^2

سؤال:

جد مساحة الشكل المُركب التالي، يتكون هذا الشكل من مستطيل ونصف دائرة.

الحل:

لإيجاد المساحة الكلية، نجد مساحة كل جزء وبعدها نقوم بجمعهم معاً.

= الطول · العرض

= 20 ·30 = 600 mm²

مساحة الدائرة:

S = πR² = π·R·R

S = π·10·10 = 100 π

S = 314 mm²

_{نصف دائرة}S =  mm²

_{المساحة الكلية} S = 600 + 157 = 757 mm²

سؤال:

الرسم يصف ملعب كرة قدم المكون من مربع مساحته 144 م²  ونصفا دوائر.

جد ما هو محيط ومساحة الملعب ؟

الحل:

Sمربع = 144 ==> الضلع = 12

دائرة S = π·6·6 = 36 π     = م^2113.04  الكليةS = 144 + 36 π       = 144 + 113.04 = م^2257.04

سؤال:

في الشكل المعطى دائرتان، لهما مركز مشترك O. أنصاف أقطار الدائرتين هما: 20 سم و 10 سم. جد مساحة الحلقة (المنطقة الملونة).

الحل:

T = S _{الكبيرة} –  S_{الصغيرة ة}

T = π·10·10  –  π·5·5

T = 100π  –   25π  = 75π  

سؤال:

احسبوا المساحة الرمادية لكل واحدة من الاشكال التالية:

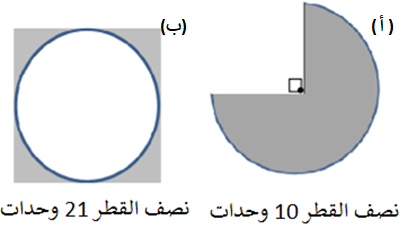
الحل:

( أ )

S_دائرة = π·r² =  π·r·r

S_دائرة = π·10·10 = 100π = 100·3.14=_وحدات314

S_رمادي =

(ب)

S_مربع = 42·42=وحدة1764

S_دائرة = π·r² =  π·21·21 = وحدات1384.74

S_رمادي  = S_مربع  - S_دائرة

S_رمادي  =_وحدات1764 – _وحدات1384.74  = 379.26

سؤال:

في داخل مستطيل حُصِرت ثلاث دوائر الذي نصف قطر كل واحد منهم هو 1.4 م.

إحسبوا المساحة المُشار لها باللون الرمادي؟

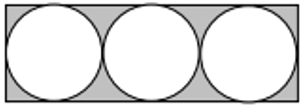
الحل:

عرض المستطيل:  2·1.4 = 2.8

طول المستطيل: مكون من 3 أقطار أو 6 مرات نصف قطر ، 6·1.4 = 8.4

مساحة المستطيل: 8.4·2.8=23.52

مساحة الــ 3 دوائر: 3·(pi1.4·1.4)=18.463

المساحة الرمادية:  23.52 – 18.463 = 5.0568

طريقة أخرى وأبسط

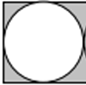
نحسب المساحة الرمادية التي في الشكل ونضربها بــ 3

3·(S _مربع – S _دائرة) =

3·(2.8·2.8 – π·1.4·1.4)

3·(7.84 – 6.1544)

3·1.6857 = 5.0568

سؤال:

معطى 3 مربعات متطابقة، بكل واحد من هذه المربعات رُسِمَت دوائر متطابقة ومتماسة لبعضها البعض.

في أي من هذه الأشكال المساحة الملونة باللون الرمادي هي الأكبر ولماذا ؟

                    (ا)                                       (ب)                                              (ج)

الحل:

نفرض أن طول ضلع المربع 30

30·30 – π·15·15 = 900 - 225π = 193.5	(أ )
30·30 – π·7.5·7.5 = 900 – 56.25π = 723.37	(ب)
30·30 – π·5·5 = 900 – 25π = 821.5	(ج)

نستنتج: كلما إزداد عدد الدوائر تكبر مساحة المنطقة الرمادية

سؤال:    (الاشكال من تصميمي)

جد مساحة كل شكل نفرض أن نصف القطر R=10

( أ )	(ب)	(ج)
( د )	(هـ)	(و)
(ز)	(ح)

سؤال:

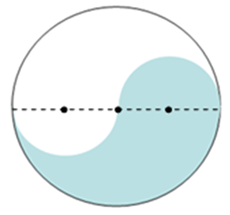
في الرسمة التي أمامك مساحة الدائرة هي A. ما هي مساحة الشكل الملون اللذي في الدائرة؟

سؤال

جد طول نصف قطر دائرة (r) مساحتها S سم²

الحل:  ( b ) 

Daliaty School – Copywrite  2023

wahbem@gmail.com | https://daliaty.com

<meta name="viewport" content="width=device-width, initial-scale=1">