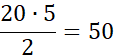|
سؤال
|
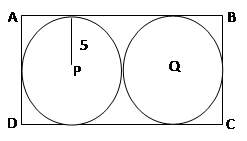
معطى ABCD
مستطيل.
لكل واحد
من الدوائر P و Q نصف
قطر طوله 5 سم.
ما هي
مساحة
المستطيل ABCD ?
أ)
500 ب) 50 ج) 200
د) 60
|
|
الحل: (ج)
|
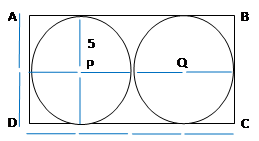
طول المستطيل يعادل 4
مرات من طول نصف قطر الدائرة،
عرض المستطيل يعادل 2
مرات من طول نصف قطر الدائرة.
|
طول المستطيل:
|
4
∙ 5 = 20
|
|
عرض المستطيل:
|
2 ∙ 5 = 10
|
من هنا مساحة المستطيل: 200
سم2
= 20 ∙ 10
|
|
سؤال
|
معطى ABCD
مستطيل.
لكل واحد
من الدوائر P و Q نصف
قطر طوله 5 سم.
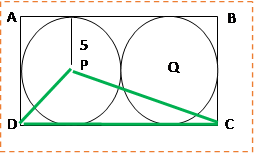
ما هي مساحة المثلث PDCΔ ?
أ) 500 ب) 50 ج) 100
د) 40
|
|
الحل: (ب)
|
طول قاعدة المثلث تعادل طول المستطيل وقيمتها 20
سم (DC=20).
ارتفاع المثلث يعادل نصف قطر الدائرة وقيمته 5
سم.
مساحة
المثلث PDCΔ:
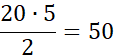
|
سؤال
|
معطى دائرة
نصف قطرها
يساوي 10 سم احسب مساحتها.
|
|
سؤال
|
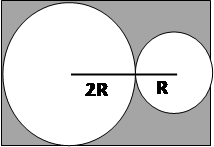
معطى
دائرتان.
الصغرى نصف
قطرها R
والكبرى
نصف قطر 2R
(ضعفي الصغرى)
أ) جد محيط
الدائرتين.
ب) جد مساحة
الدائرتين.
ج) جد
المساحة
الغامقة
(المحصورة
بين الدائرتين)
|
|
سؤال
|
جد
محيط الشكل
التالي:
|

|
سؤال
|
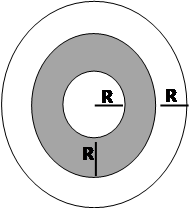
الشكل
مكون من 3
دوائر.
البعد
بين الدوائر
متساوي
وقيمة كل
واحد R.
جد
المساحة
المخططة:
|
|
سؤال
|
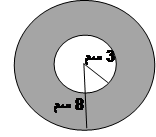
امامك
دائرتين
لهما نفس
المركز.
نصف
قطر الدائرة
الاولى 8 سم ونصف
قطر الدائرة
الاخرى 3 سم.
ما
المساحة
المظللة?
i.
64p سم² ii.
55p سم²
iii. 25p سم² iv. 9p سم²
|
|
سؤال
|
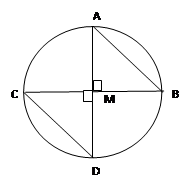
القطران
في الدائرة
التي مركزها M متعامدان.
علل لماذا
AB
= CD
|
|
سؤال
|
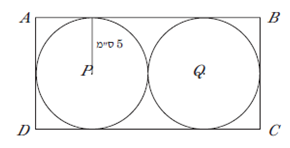
ABCD مستطيل.
لكل
دائرة P, Q نصف
قطر طوله 5 سم.
ما هي
مساحة
المستطيل? (أحط
بدائرة
الإجابة
الصحيحة):
50 سم² - 60 سم² - 100 سم² - 200 سم²
|
|
سؤال
|
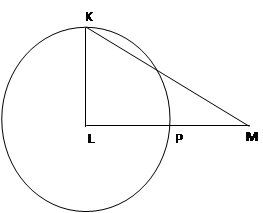
القطعة KL تمثل نصف قطر الدائرة في الرسم التوضيحي أمامك.
النقطة L مركز الدائرة.
KLM مثلث قائم الزاوية، ∢L = 90°.
النقطة P تقع على محيط الدائرة وعلى القطعة LM بحيث أن: LP = PM
مساحة الدائرة تساوي 25p سم2.
جد مساحة المثلث KLM.
بين حساباتك.
|
|
سؤال
|
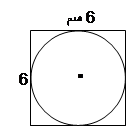
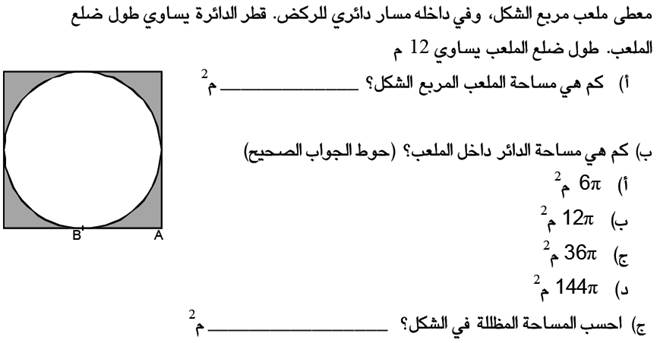
في الشكل أمامك مربع يمس دائرة.
طول ضلع المربع هو 6 سم.
أ) جد نصف قطر الدائرة.
ب) احسب مساحة الدائرة داخل المربع.
(إنجاز 2011)
|
|
سؤال
|
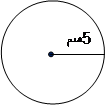
احسب مساحة الدائرة في الشكل:
|
|
سؤال


سؤال


سؤال
|
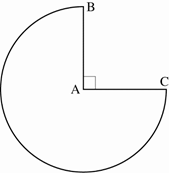
الشكل
أمامك هو جزء
من دائرة
مركزها
النقطة A.
معطى: ∢BAC
= 90°,
10 سم AB =
ما
هي مساحة
الشكل بالسم2
؟
أ. 15p
ب. 20p
ج. 75p
د. 100p
(2013)
|
|
سؤال
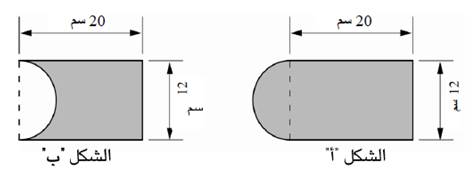
أمامك
شكلان:
الشكل
أ هو مستطيل
ألصق له نصف
دائر.
الشكل ب هو
مستطيل قُص
منه نصف
دائرة.
أ. أشر
إلى الادعاء الصحيح:
i. محيط
الشكل (أ) أصغر من
محيط الشكل ب.
ii. محيط
الشكل (أ) يساوي
من محيط
الشكل ب.
iii. محيط
الشكل (أ) أكبر
من محيط
الشكل ب.
ب. ما
هي مساحة
الشكل (أ)
بالسم2؟
أ. 12p + 240 ب. 18p + 240 ج. 24p + 240 د.
36p + 240
ج. احسب
مساحة الشكل
ب بالسم2.
(2013)
|