|
صفحة
البيت | wahbem@gmail.com |
(1) الزوايا
المتجاورة
تعريف:
هما زاويتان
لهما ساق
مشتركة
والساقين
الأخريين على أستقامة
واحدة.
الخاصية:
مجموع
الزاويتان
المتجاورتان
180
أمثلة:
|
|
|
ملاحظة:
|
ليست
زوايا
متجاورة |
|
ولكن
يتحقق أن: ![]()
أنواع
الزوايا
الناتجة:
|
يتحقق
أن إحدى
الزاويتين
تكون حادة
والأخرى منفرجة. |
|
سؤال: هل
يمكن أن يتحقق
أن الزاويتين
المتجاورتين متساويتين؟
|
يتحقق
مساواة بين
الزاويتين
المتجاورتين
عندما يتحقق
التعامد بين
المستقيمين |
|
مثال:
|
جد
مقدار
الزاوية:
|
الحل:
|
مثال:
|
جد
مقدار
الزاوية:
|
الحل:
|
سؤال: (زوايا
متجاورة)
جد
قيمة x:
|
(a)
110 (a) 180 (c) 70 (d) 80 |
|
الحل ( c ) مجموع
الزاويتان 180،
لأنهما
تكونان زاوية
مستقيمة: x + 110 =180
لذلك x=70
سؤال: (زوايا
متجاورة)
جد
قيمة x:
|
(a) 40 (b) 140 (c) 180 (d) 30 |
|
الحل ( b ) مجموع
الزاويتان 180،
لأنهما
تكونان زاوية
مستقيمة: x + 140 =180 لذلك x=40
سؤال: (زوايا
متجاورة)
|
(a) 75 درجة (b) 15 درجة (c) 180 درجة (d) 105 درجة |
ما
هي قيمة
الزاوية y
|
الحل ( d ) مجموع
الزاويتان 180،
لأنهما
تكونان زاوية
مستقيمة: y + 75 =180 لذلك y=105
مثال:
جد
قيمة x
واحسب
قيمة الزاوية:
|
|
الحل:
2x – 18 + 6x - 2 = 180 2x + 6x = 180 + 18 + 2 8x = 200 x = 25 |
مثال:
جد
قيمة x
واحسب
قيمة الزاوية:
|
|
الحل: 2x + 20 + x – 50 = 180 2x + x = 180 - 20 + 50 3x = 210 x = 210:3 x = 70 |
مثال:
|
جد
قيمة x واحسب
قيمة
الزاويتين:
|
|
3x + 10 + 4x – 40 = 180 3x + 4x = 180 -10 + 40 7x = 210 X = 210 : 7 X = 30 |
سؤال
|
احسب
مقدار كل من
الزاويتين
المُشَار
لهما بـ a و بـ b a = ____°, b = ____° |
|
سؤال
(سابع-إنجاز-17-5-2010 )
AB
و KL مستقيمان متقاطعان. أجب بحسب المعطيات في الرسم.
|
|
أ) ما هي قيمة
الزاوية 1 بالدرجات ؟
الجواب: °_______________
ب) ما هي قيمة الزاوية 2 بالدرجات؟ الجواب: °_______________
سؤال (2013)
a
و b
زاويتان متجاورتان. احسب مقدار كل منهما، إذا كان:
أ. b أكبر
من a
بــ 70°
ب. b تساوي
3 أضعاف a
|
|
سؤال
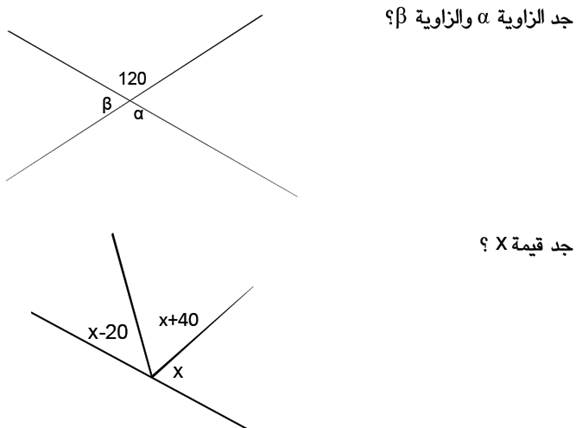
سؤال
احسب
قيمة الزاوية Z و وقيمة
الزاوية x
|
|
سؤال
MP
هو
خط مستقيم.
ما
هو مقدار
الزاوية
KLP المبينة
في الرسم؟
بين
طريقة الحل.
|
|
سؤال

سؤال

سؤال
معطى أن مستقيمان يتقاطعان في النقطة O.
a + b + g = 280°.
ما هو مقدار الزاوية b?
|
|
الإجابة:
معطى: a + b + g = 280°
مجموع الزوايا الأربعة: 360° (مجموع زوايا الدائرة 360).
من هنا الزاوية الرابعة: 360 – 280 = 80
الزاوية b أيضا قيمتها 80 (زوايا متقابلة بالرأس متساوية).
سؤال
معطى في
الرسم MP
هو خط مستقيم.
ما هو مقدار
الزاوية KLP
المبينة في
الرسم؟ بين
طريقة الحل.
أ)
80 ب) 140 ج) 180
د) 40
|
|
الإجابة: (ب)
KLP=180∢KLM+∢ (مجموع زاويتين متجاورتين 180°)
المعادلة الملائمة: x+x+100=180
2x+100=180
2x=80
x=40
من هنا: KLP = x + 100∢
40 + 100
= 140
لذلك الزاوية المطلوبة: 140
سؤال
في
الرسم الذي أمامك:
MP
و KT مستقيمان يتقاطعان في النقطة L.
∢KLP
اكبر بضعفين (بـ 2 مرات)
من الزاوية ∢KLM.
LR
منصف للزاوية ∢KLP.
أ)
اشرح لماذا KL منصف الزاوية ∢MLR
ب)
احسب قيمة الزاوية ∢PLT.
|
|
الإجابة:
أ) لكي نثبت أن KL منصف الزاوية ∢MLR علينا أن نثبت أن:
∢KLM=∢KLR
نرمز للزاوية ∢KLM بـ x
من هنا ∢KLP=2x (بموجب المعطى)
∢KLR=∢RLP=x (لأنه معطى LR منصف للزاوية ∢KLP)
نستنتج: ∢KLM=∢KLR=∢RLP=x (أنصاف زوايا متساوية).
نستنتج: KL منصف للزاوية ∢MLR وهو المطلوب.
ب) نحسب قيمة الزاوية ∢PLT:
مجموع الزوايا الثلاث 180 (لأنهم يشكلون زاوية مستقيمة).
قيمة كل زاوية: 180 : 3 = 60
∢PLT=∢KLM=60 (زوايا متقابلة بالرأس متساوية)
سؤال

سؤال
معطى
النقاط A,B,C التي تقع على مستقيم
واحد.
الزاوية ∢MBC
مقدارها 60
درجة.
الزاوية∢DBA مقدارها
50 درجة.
جد مقدار الزاوية ∢DBM.
|
|
سؤال
AC و BD
مستقيمان
يتقاطعان في
النقطة M.
AMB=60 ![]()
جد
باقي الزوايا
؟
|
|
سؤال
معطى
في الرسم
زاويتان
متكاملتان
أ)
جدوا
قيمة x
ب) جدوا
قيمة كل زاوية
من الزوايا المتكاملة.
|
|
سؤال
|
معطى
مستقيمان
متقاطعان. جد قيم
الزوايا
الآتية: x=______ y=______ ______= z |
|
سؤال
جد مقدار
الزوايا
|
(أ)
|
(ب)
|
(ج)
|
سؤال
احسب
مقدار
الزاوية
المشار اليها
|
|
سؤال (إنجاز
2011)
القطعتان
AB
وCD
تتقاطعان في E.
القطعة GM تقطع
القطعة CD في
النقطة M.
أكمل مقدار كل
من
الزاويتين a و b
بحسب
المعطيات على
الرسم.
فسر
أ) a =
______º لأن ________________
ب) b =
______º لأن _______________
|
|


Hermes Math - Copywrite – 2021
wahbem@gmail.com





























