هرمس ماث - Hermes Math

  صفحة البيت | wahbem@gmail.com

 

 

 

 

 

 واعلمي يا نفس أنَّ الإنسان لم يُخلَق لمعنًى من المعاني إلاَّ للعلم والعمل به (هرمس) 

 

 

                                                                                                                                                                                                                                                                                                           

 

 

 

 

 

 

 

 

سؤال:

 

جد قيمة x:

 

 

(a)

80

(b)

50

(c)

40

(d)

130

 

 

 

الحل ( c )

 

  

 

 

سؤال:

 

جد قيمة x:

 

 

(a)

30

(b)

170

(c)

70

(d)

110

 

 

 

الحل ( c )

 

 

  

 

 

سؤال:

 

جد قيمة x:

 

 

(a)

140

(b)

40

(c)

45

(d)

30

 

 

 

الحل ( c )

 

 

  

 

 

سؤال:

 

جد قيمة x:

 

 

(a)

 

(b)

 

(c)

 

(d)

 

 

 

 

الحل ( c )

 

 

  

 

 

سؤال:

 

جد قيمة x:

 

 

(a)

 

(b)

 

(c)

 

(d)

 

 

 

 

الحل ( c )

 

 

 

  

 

 

سؤال:

 

 

 

الزوايا التي أمامك هي:

 

myStudiyo Media

 

 

(a)

متتاليتان (أحادية الجانب)

(b)

متناظرة

(c)

متبادلة

(d)

متقابلة بالرأس

      

 

 

الحل ( c )

 

 

  

 

 

سؤال:

 

الزوايا التي أمامك هي:

 

 

 

myStudiyo Media

 

(a)

متبادلة

(b)

متناظرة

(c)

متجاورة

(d)

متقابلة بالرأس

      

 

الحل ( b )

 

 

  

 

 

 

سؤال

 

في الرسم أمامك معطى:

m ççp       t ççk      1 = 75°∢  

احسب مقدار الزاوية 2. اعرض طريقة الحل.

 

(2013)

 

 

 

 

سؤال

 

 

معطى: k || m.

احسب مقدار الزاوية α.

اعرض طريقة الحل.

 

(2013)

 

 

 

 

سؤال

 

 

معطى: k || m.

احسب مقدار الزاوية α.

 اعرض طريقة الحل.

 

 

(2013)

 

 

 

 

سؤال

 

 

 

 

 

 

سؤال

 

 

زوايا (يشمل مجموع الزوايا في المثلث والشكل الرباعي)

 

 

 

 

ما هو مقدار الزاوية  a؟

i.      35°      ii.  40° 

iii.   55°    iv  .  60°

 

 

 

 

 

 

سؤال

 

 

AB || CD، EF يقطع القطعتينAB  و CD

ما مقدار الزاوية  a ؟

تذكر: مجموع الزوايا المتجاورة هو 180


i.      25°      ii.  65°
iii.   125°     iv.  155°

 

 

 

 

 

 

سؤال

 

 

أمامك شبه منحرف .
AB || CD،  AC ^ BC،

 AC ينصّف الزاوية A.
ACD = 30° ∢
احسب مقدار الزاويتين  B, D.
بَيِّن طريقة الحساب وفسّر.

 

 

 

 

 

سؤال

 

 

معطى مستطيل ABCD وفي داخله مثلث ABE.
بناءً على المعطيات المبينة في الرسم،

جد مقدار الزاوية x.

بين طريقة الحل.

 

 

 

 

 

 

سؤال

 

 

معطى المستطيلان ABCD å- KLMT.

أطوال أضلاع المستطيل ABCD هي:
 
 

أطوال أضلاع المستطيل KLMT هي:

 
 

 

أ‌)       اشرح لماذا ∢KPD هي زاوية قائمة

ب‌)اشرح لماذا الشكل الرباعي KLEP هو مستطيل

ت‌)احسب محيط المضلع الناتج من المستطيلين.

ث‌)احسب مساحة المضلع الناتج من المستطيلين.

 

 

 

 

سؤال

 

 

 

 

 

 

 

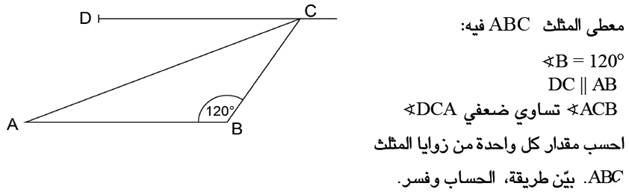
سؤال

 

معطى مستطيل ABCD وفي داخله مثلث ABE.

بناءً على المعطيات المبينة في الرسم، جد مقدار الزاوية x. بين طريقة الحل.

 

 

الإجابة:

AEB∢CBE=∢ (زوايا متبادلة متساوية، بين مستقيمين متوازيين)

لذلك: x=24°

 

 

 

 

سؤال

 

 

معطى مستطيل ABCD وبداخله مثلث rEDC

استنادا للمعطيات التي في الرسم

احسب قيمة الزاوية Ð ECB ? 

 

     أ) 100     ب) 180     ج) 80       د) 50   

 

 

الإجابة: (د)        

ÐAEC + ÐDEC = 180  (زوايا متجاورة جمعها 180)
x + 80 + x = 180

2x + 80 = 180 

2x = 100

x=50

من هنا:  ÐECB = ÐDEC = 50 (الزوايا المتبادلة متساوية).

 

 

 

 

  

 

 

 

 

 

 

   

 

 

                            

 

 

 

Hermes Math - Copywrite – 2021

wahbem@gmail.com