|
صفحة
البيت | wahbem@gmail.com |
واعلمي
يا نفس أنَّ
الإنسان لم
يُخلَق لمعنًى
من المعاني
إلاَّ للعلم
والعمل به
(هرمس)
اختبار مفمار – فرق
إنجاز - 2010
سؤال1
في
هيئة المحاور أمامك عُيّنت 4 نقط، أي نقطة منها إحداثياتها (-6,3) ?
|
(A) T (B) R (C) P
(D) Q
|
|
الحل: (
b )
النقطة (-6,3) إحداثياتها: ![]() ،
،
من هنا (-,+) وهي في
التربيع
الثاني.
النقطة
الملائمة R
سؤال2
أي من
بين التعابير
الآتية قيمته
تساوي قيمة
التعبير ![]() ?
?
(A) ![]() (B)
(B) ![]() (C) m4 (D) 4(m
+ 1)
(C) m4 (D) 4(m
+ 1)
الحل: ( A )
اختصار تكرار الجمع هو الضرب: ![]()
اختصار تكرار الضرب القوى: ![]()
سؤال3
احسب: ![]()
(A) 10 (B)
14 (C)
2 (D) -2
الحل: ( C
)
الضرب قبل القسمة: ![]()
سؤال4
احسب: ![]()
(A) 12
(B) 19 (C) 4
(D) -4
الحل: (
D )
![]()
![]()
سؤال5
احسب: 24 : 23 =
(A)
4 (B) 36 (C)
1 (D) 3
الحل: (
D )
![]()
![]()
سؤال6
احسب: ![]()
(A)
12 (B) -6 (C)
-12 (D) 3
الحل: (
A )
![]()
![]()
![]()
سؤال7
أي
عدد من
الأعداد
الآتية هو حل
المعادلة: ![]() ?
?
(A)
1 (B) 2 (C) -3 (D) -2
الحل: (
D )
![]()
![]()
![]()
سؤال8
في وعاء 11 كرة سوداء، و 5 كرات بيضاء و
3 كرات رمادية.
ما هو الاحتمال لإخراج كرة سوداء من الوعاء دون أن ننظر فيه؟
|
|
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
الحل: (
D )
|
عدد الكرات التي في السلة: |
11 + 5 + 3 = 19 |
يوجد 11 كرة سوداء من بين 19 كرة
الاحتمال لإخراج كرة سوداء: ![]()
سؤال9
عُينت
على محور
الأعداد
النقط A, B, C, D.
النقطة
x غير
معيّنة على
المحور، هي
تدل على عدد
سالب أكبر من -6
أين
تقع النقطة x
؟

(A)
عن يسار A (B)
بين
A و- B
(C) بين B
و- C
(D) بين C
و- D
الحل: (
B )
معطى أن العدد سالب
وأكبر من -6 ، لذلك
العدد بين صفر
و -6
أي بين A
و B.
سؤال10
أمامك
أبنية مكونة
من مكعبات لها
نفس الحجم.
ثلاثة
أبنية
متساوية في
الحجم ومبنى
واحد له حجم
مختلف.
جد
المبنى الذي
له حجم مختلف.
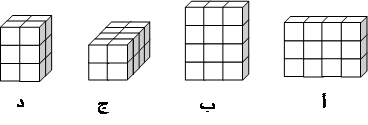
(A)
شكل ( د )
(B) شكل ( أ ) (C) شكل ( ج) (D) شكل (ب)
الحل: (
C )
تذكر حجم الصندوق: الطول![]() العرض
العرض ![]() الارتفاع
الارتفاع
عدد المكعبات في شكل
(أ): ![]()
عدد المكعبات في شكل
(ب): ![]()
عدد المكعبات في شكل
(ج): ![]()
عدد المكعبات في شكل
(د): ![]()
شكل (ج)
هو الذي له حجم مختلف.
سؤال11
حل
المعادلة التالية: ![]()
(A)
15 (B) 6 (C) 30
(D) ![]()
الحل: (
A )
![]()
![]()
![]()
سؤال12
حل
المعادلة التالية: 
(A)
![]() (B) 2 (C)
24 (D) 8
(B) 2 (C)
24 (D) 8
الحل: (
D )
|
|
سؤال13
(أ) لدى
أمير عدد من
الكتب يساوي ضعفي عدد كتب
عادل.
![]() يمثل عدد
كتب عادل.
يمثل عدد
كتب عادل.
اكتب
تعبيرًا
جبريًا يمثل
عدد كتب أمير.
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
(ب) لدى
الاثنين معًا
63 كتابًا.
كم
عدد كتب عادل
؟ بيّن
طريقة الحل.
(A)
21 (B) 12
(C) 24
(D) 6
الحل:
(أ) الإجابة: ( B )
عدد كتب عادل:
x
عدد كتب أمير:
2x
(ب) الإجابة: ( A )
المعادلة الملائمة: ![]()
نحل المعادلة:
(ندمج الحدود المشتركة)
|
|
سؤال14
إذا
كان ![]() ، ما هي
قيمة التعبير
، ما هي
قيمة التعبير ![]() ؟
؟
بيّن
طريقة الحساب.
(A) -52 (B) -10 (C)
10 (D) 90
الحل: (
B )
نعوض x=7 في التعبير ![]() :
:
![]()
![]()
سؤال15
أمامك مثلث محيطه 35 سم.
احسب أطوال أضلاع المثلث بالاعتماد على المعطيات المبيّنة في الرسم.
|
(A) 4, 8, 7 (B) 8, 11, 16 (C) 8,
12, 15 (D) 6,
8, 21 |
|
الحل: (
B )
محيط المثلث هو حاصل
جمع الثلاث أضلاع:
|
|
نفحص
الحل:
|
الضلع
الأول: الضلع
الثاني: الضلع
الثالث: انتبه
أن حاصل
جمعهم: |
<== 8 <== 2 <== 8+3=11 8+16+11=35 |
وهذا ملائم لمعطيات المسألة.
سؤال16
معطاة
المعادلة: ![]() .
.
أي
معادلة من بين
المعادلات
الآتية
مكافئة للمعادلة
المعطاة ولها
نفس الحل؟
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
الحل: (
C )
لكي نعرف الإجابة ننفذ
فقط الخطوة الأولى من حل المعادلة:
|
|
لذلك الإجابة (ج)
سؤال17
AB و KL
مستقيمان متقاطعان.
أجب بحسب المعطيات في الرسم.
احسب ما هي قيمة الزواية x و
y
بالدرجات ؟
|
(A) x=160 y=20 (B) x=20 y=160 (C) x=80 y=120 (D) x=160 y=80 |
|
الحل: (
B )
|
|
|
بالنسبة للزاوية x: |
x+160=180 |
(زوايا متجاورة جمعها 180) |
من هنا x=20
بالنسبة للزاوية y: قيمتها 160 (الزوايا المتقابلة بالرأس متساوية)
سؤال18
اشترت أمال x
قناني شراب ودفعت 18 شاقلاً ثمنًا لها.
ما هو سعر
القنينة الواحدة ؟
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
\
الحل: (
D )
نفرض أن أمال
اشترت 6 قناني (بدلاً من x) ودفعت ثمنهم 18 شاقلاً.
في هذه الحالة يكون
سعر القنينة: ![]()
من هنا ثمن
القنينة: 
لذلك الإجابة: ![]()
سؤال19
في هيئة المحاور التي
أمامك عُيّنت 3
نقط.
جد على الشكل نقطة
رابعة R بحيث تحصل على
مستطيل.
|
إحداثيات النقطةR هي: (A) R(7 , 6) (B) R(3 , 6) (C) R(6 , 7) (D) R(4 , 6) |
|
الحل: (
C )
النقطة المطلوبة هي النقطة الحمراء. إحداثيات النقطة R(6,7)
|
|
سؤال20
(أ)
احسب
مساحة الشكل المرسوم أمامك (بيّن طريقة الحساب).
|
|
(A) 96 (B)
105 (C) 69 (D) 40
(ب)
احسب محيط الشكل المرسوم (بيّن
طريقة الحساب).
أ) 40
ب) 69 ج)
112 د) 32
الحل ( أ ) : ( C )
الحل (ب) : ( A )
( أ ) الحل: ( C )
|
|
مساحة المستطيل الصغير: ![]()
مساحة المستطيل الكبير: 12∙5=60
مساحة الشكل: 69 سم2 60+9=
(ب) محيط الشكل: ![]()
سؤال21
مجموع عددين يساوي 14.
أحد العددين أكبر من الآخر بـ 8.
ما
هما العددان؟ (بيّن طريقة الحساب)
قيمة العدد الأصغر:
(A) 11 (B) 4 (C) 2 (D) 3
الحل: (
D )
العدد الأول: x
العدد الثاني: ![]()
مجموع العددين: ![]()
نحل المعادلة:
|
2x+8=14 /-8 2x=6 /:2 x=3 |
العدد الصغير: 3،
والعدد الكبير: 3
+ 8 = 11
سؤال22
أمامك
الخط البياني
الذي يصف نسبة
الرطوبة في غرفة
ما، التي قيست
في ساعات
الصباح.
|
|
(أ) كم كانت نسبة الرطوبة في الغرفة الساعة 8 ؟
أ) 0 ب)
40 ج) 45 د) اقل من 40
(ب)
بالاعتماد على الخط البياني، كم مرة بين الساعة 6:00 إلى الساعة
12:00 كانت نسبة الرطوبة 30% بالضبط ؟
أ) مرة
واحدة ب) مرتان ج) 3 مرات د) 4 مرات
(ج) نسبة
الرطوبة
في الغرفة بين الساعة 10 إلى الساعة 12 صباحًا:
أ) ارتفعت ب)
انخفضت ج) على
وتيرة ثابتة د)
ثابتة
الإجابة:
الحل: (أ) (ج) ، (ب)
الحل: (ب) ،
(ج)
الحل: (ب)
سؤال23
أمامك مثلث قائم الزاوية ABC.
احسب مقدار الزاوية ∢C في المثلث المعطى.
|
(A) 32 (B) 90
(C) 58 (D) 38 |
|
الحل: (
C )
في
مثلث قائم الزاوية مجموع الزاويتين الحادتين °90
![]()
![]()
سؤال24
أمامك مثلث قائم الزاوية ABC.
احسب مساحة المثلث ABC, بالاعتماد على القياسات المسجلة على الشكل.
|
(A) 160 سم2 (B) 26 سم2 (C) 40 سم2 (D) 80 سم2 |
|
الحل: (
D )
مساحة المثلث:  <==
<== ![]()
سؤال25
رَتبوا عيدان ثقاب بطريقة ما كما في الشكل:
|
|
(أ) إذا استمرينا في البناء بنفس الطريقة، كم عود ثقاب يكون في الشكل 4؟
إذا استمرينا في البناء بنفس الطريقة، كم عود ثقاب يكون في الشكل 10؟
أ) 15, 30 ب) 15,
43 ج) 15, 33
د) 18, 33
(ب) في الشكل 50 يوجد 153 عود ثقاب.
كم
عود ثقاب يكون في الشكل 51 ؟
(أ) 156 (ب) 150 (ج) 163
(د) 193
(ج) أكتب تعبيراً جبرياً يصف العلاقة بين رقم الشكل وعدد عيدان الثقاب ؟
(أ) 3(n+3) (ب)
3n+3 (ج)
3n+2 (د) 3n
الحل: (
B )
(أ) الإجابة: (ج)
|
|
في
كل شكل عدد عيدان الثقاب أكثر بــ 3 عيدان عن الشكل الذي يسبقه.
في
الشكل الرابع يكون 15 عود ثقاب (12+3=15).
في
الشكل العاشر يكون 10∙3+3=33
من
هنا الإجابة هي (ج).
(ب)
الإجابة:
(أ)
عدد عيدان الثقاب في شكل 51 أكثر بـ 3 عيدان عن الشكل الذي سبقه.
لذلك: 153 +
3 = 156
(ج) الإجابة: (ج)
|
|
لكي تجد العلاقة المطلوبة تمعن في الجدول التالي:
|
عدد عيدان الثقاب في الشكل |
شكل رقم |
|
3+3=1∙3+3=6 |
1 |
|
3+3+3=2∙3+3=9 |
2 |
|
3+3+3+3=3∙3+3=12 |
3 |
|
3+3+3+3+3=4∙3+3=15 |
4 |
|
3+3+……3+3=n∙3+3 |
n |
من
هنا الإجابة هي (ج).


Hermes Math - Copywrite – 2021
wahbem@gmail.com


















